Wenn Sie A/B Tests im Hinblick auf eine verbesserte User Experience durchführen, möchten Sie letzten Endes Ihren Umsatz steigern. Wir sprechen jedoch eher von der Verbesserung der Conversion Rates (d.h. die Verwandlung eines Besuchers in einen Käufer).
Wenn Sie die Conversion Rate erhöhen, steigern Sie automatisch den Umsatz und die Anzahl der Transaktionen. Aber dies ist nur eine Methode von vielen – den „durchschnittlichen Warenkorbwert“ steigern ist eine andere Taktik. Dieser Ansatz wird jedoch weniger genutzt. Warum? Weil es immer noch relativ schwierig ist, eine Veränderung des durchschnittlichen Warenkorbwerts zu messen.
Ein Problem der Messung und Statistik
Wenn wir im Zusammenhang mit dem durchschnittlichen Warenkorbwert über statistische Tests sprechen, was meinen wir dann? In der Regel beziehen wir uns auf den Mann-Whitney-U-Test (auch als Wilcoxon bezeichnet), der in bestimmten A/B-Testsoftwarelösungen verwendet wird, einschließlich AB Tasty. Ein „Must Have“ für jeden, der seine Conversion Rate steigern möchte. Dieser Test zeigt die Wahrscheinlichkeit auf, dass die Variante B mehr Gewinn erzielt als die Originalversion. Es ist jedoch unmöglich, die Höhe dieses Gewinns zu bemessen – und vergessen Sie nicht: mit den Strategien zur Steigerung des durchschnittlichen Warenkorbwerts sind wahrscheinlich Kosten verbunden. Deshalb ist es besonders wichtig, dass sich die Kosten im Vergleich zum Gewinn lohnen.
Wenn Sie zum Beispiel ein Tool für eine Produktempfehlung testen möchten, müssen Sie sicher sein, dass die damit verbundene Umsatzsteigerung die Kosten für dieses Tool übersteigen…
Allerdings werden Sie feststellen, dass dies ein kniffliges Problem ist, das auf den ersten Blick nicht einleuchtet …
Nehmen wir ein konkretes Beispiel: Man berechnet ahnungslos den durchschnittlichen Warenkorbwert direkt. D. h. die Summe aller Warenkorbwerte geteilt durch die Anzahl der Warenkörbe. Und das ist nicht falsch, da diese Rechnung Sinn ergibt. Sie ist jedoch nicht besonders genau! Der wahre Fehler ist, dass hier Äpfel mit Birnen verglichen werden und geglaubt wird, der Vergleich würde stimmen. Machen wir es also richtig und nehmen wir die genauen Daten eines durchschnittlichen Warenkorbs, um den Gewinn des durchschnittlichen Warenkorbwerts zu simulieren.
Hier unsere Vorgehensweise:
- Nehmen wir P, eine Liste von Warenkorbwerten (echte Daten, die auf einer E-Commerce-Website und nicht während eines Tests gesammelt wurden).
- Wir mixen diese Daten und teilen sie in zwei Gruppen, Gruppe A und Gruppe B.
- Wir lassen Gruppe A so wie sie ist: unsere Bezugsgruppe, die wir „das Original“ nennen.
- Rechnen wir 3 Euro auf alle Werte in Gruppe B hinzu, der Gruppe, die wir „Variante“ nennen und bei der wir das Experiment durchgeführt haben (beispielsweise mit einem System zur Produktempfehlung für Besucher der betreffenden Website).
- Jetzt können wir einen Mann-Whitney-Test durchführen, um sicherzustellen, dass der zusätzliche Gewinn tatsächlich signifikant ist.
Anhand dieser Zahlen werden wir die durchschnittlichen Werte der Listen A und B und die Differenz berechnen. Unbedarft erwarten wir jetzt einen Wert um 3 Euro (die dem Gewinn entsprechen, den wir in der Variante hinzugefügt haben haben). Aber das Ergebnis stimmt nicht. Warum? Das sehen wir unten.
Wie wird der durchschnittliche Warenkorbwert berechnet?
In der folgenden Grafik werden die oben erwähnten Werte aufgeführt: d. h. 10.000 durchschnittliche Warenkorbwerte. Die (horizontale) X-Achse stellt einen Warenkorbwert dar; die (vertikale) Y-Achse wie oft dieser Wert bei den Daten festgestellt wurde.
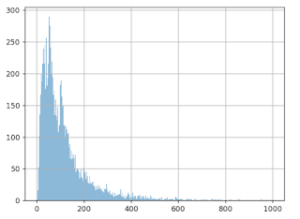
Offensichtlich liegt der am häufigsten auftretende Betrag bei rund 50 Euro. Rund 100 Euro ist ein weiterer Spitzenwert. Beträge über 600 Euro sind kaum vorhanden.
Nach dem Mischen der Liste dieser Beträge unterteilen wir sie in zwei Gruppen (5000 Daten für Gruppe A und 5000 für Gruppe B).
Anschließend rechnen wir 3 Euro zu jedem Wert in Gruppe B hinzu und erstellen die Grafik für beide Gruppen, A (blau) und B (orange):
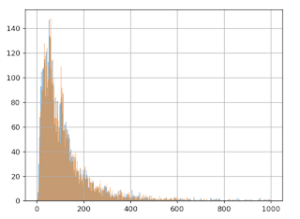
Wir stellen auf der Grafik sofort fest, dass die hinzugefügten 3 Euro keine Auswirkung auf Gruppe B haben: die orangene und blaue Linie sehen relativ identisch aus. Selbst wenn in die Grafik hineingezoomt wird, ist der Unterschied kaum zu bemerken:
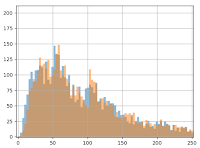
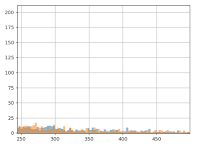
Aber der Mann-Whitney-U-Test „sieht“ diesen Gewinn:

Genauer gesagt errechnet dieser Test einen p-Wert von 0,01, wodurch sich ein Konfidenzintervall von 99 % ergibt, wir also an einen Wertzuwachs von Gruppe B im Verhältnis zu Gruppe A glauben. Wir können jetzt sagen, dass dieser Gewinn „statistisch sichtbar“ ist.
Wir müssen jetzt nur die Höhe dieses Gewinns abschätzen (wobei wir wissen, dass er einen Wert von 3 Euro hat).
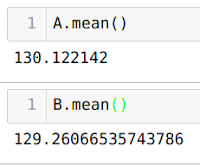
Leider ergibt sich aus dieser Rechnung nicht das erhoffte Ergebnis! Der Durchschnitt der Gruppe A liegt bei 130 Euro und 12 Cent, und bei Version B bei 129 Euro und 26 Cent. Ja, Sie haben richtig gelesen: Aus der Errechnung des Durchschnitts ergibt sich ein Durchschnittswert von B, der kleiner als der Wert von A ist. Also das Gegenteil von dem, was wir im Protokoll erstellt haben und was der statistische Test aussagt. Das bedeutet, dass wir statt 3 Euro zu gewinnen, 0,86 Cent verlieren!
Wo liegt also das Problem? Und was stimmt nun wirklich? A > B oder B > A?

Der Begriff der Extremwerte
Die Wahrheit lautet: B > A! Wie ist das möglich? Anscheinend unterliegt die Aufteilung der durchschnittlichen Warenkorbwerte „extremen Werten“. Wir sehen in der Grafik, dass die meisten Werte unter 500 Euro liegen.
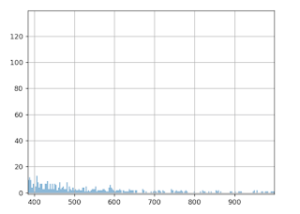
Aber bei genauerer Betrachtung erkennen wir eine Art „Longtail“, aus dem ersichtlich wird, dass der Wert von 500 Euro in manchen, wenn auch wenigen Fällen deutlich überschritten wird. Beim Berechnen der Durchschnittswerte kommen diese extremen Werte jedoch zum Tragen. Einige wenige besonders hohe Warenkorbwerte können beträchtliche Auswirkungen auf die Berechnung der Durchschnittswerte haben.
Was ist also geschehen? Bei der Aufteilung der Daten in Gruppe A und B werden diese „extremen Werte“ nicht gleichmäßig auf beide Gruppen aufgeteilt (weder anzahl- noch wertemäßig), was deshalb umso wahrscheinlicher ist, da diese Werte sehr selten vorkommen und besonders hoch sind (und stark variieren).
NB: Bei einem A/B-Test werden die Besucher der Website nach dem Zufallsprinzip den Gruppen A und B zugewiesen, sobald sie auf der Website „landen“. Uns liegen hier also dieselben Bedingungen wie bei einem Test vor.
Kann das oft passieren? Leider ja. Wir werden es sehen.
A/A Tests
Um diese Frage näher zu beantworten, brauchen wir ein Programm, das A/A-Tests automatisch erstellt, d. h. einen Test, bei dem keine Änderungen an der zweiten Gruppe vorgenommen werden (die in der Regel Gruppe B genannt wird). Ziel ist, die Genauigkeit des Testverfahrens zu prüfen. Hier unsere Vorgehensweise:
- Mixen Sie die anfänglichen Daten
- Teilen Sie sie auf zwei Gruppen gleicher Größe auf
- Berechnen Sie den Durchschnittswert jeder Gruppe
- Berechnen Sie die Differenz zwischen den Durchschnittswerten
Wenn Sie dieses Programm 10.000 Mal durchlaufen lassen und eine Grafik über die gemessenen Differenzen erstellen, erhalten Sie folgendes Ergebnis:
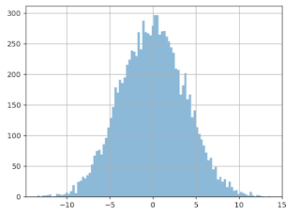
X-Achse: die gemessene Differenz (in Euro) der Durchschnittswerte von Gruppe A und Gruppe B.
Y-Achse: wie oft diese Größendifferenz festgestellt wurde.
Wir sehen, dass sich die Aufteilung um Null bewegt, was logisch ist, weil wir den Daten der Gruppe B keinen Gewinn hinzugefügt haben. Das Problem ist hier der Verlauf der Kurve: Abweichungen von mehr als 3 Euro scheinen relativ häufig zu sein. Wir können sogar davon ausgehen, dass sie auf 20 % der Fälle zutreffen. Was können wir also daraus schließen? Allein auf Basis dieser Differenz beim Durchschnittswert können wir in ca. 20 % der Fälle einen Gewinn von mehr als 3 Euro feststellen – obwohl bei Gruppe A und Gruppe B keine Änderungen in der Bearbeitung vorgenommen wurden!
Ebenso stellen wir fest, dass man laut Grafik meint, in 20 % der Fälle einen Verlust von 3 Euro pro Warenkorb zu messen … was ebenfalls nicht stimmt! Das war übrigens auch im vorherigen Experiment der Fall: Durch die Aufteilung der Daten stieg der Durchschnittswert bei Gruppe A „künstlich“ an. Die zusätzlichen 3 Euro auf alle Werte der Gruppe B konnte diesen Verlust nicht ausgleichen. Das Ergebnis? Der Anstieg von 3 Euro pro Warenkorb ist „unsichtbar“, wenn wir den Durchschnittswert berechnen. Wenn wir nur die einfache Berechnung der Differenz betrachten und entscheiden, dass unsere Grenze bei 1 Euro liegt, haben wir eine Chance von etwa 80%, an einen Gewinn oder Verlust zu glauben… den es nicht gibt!
Warum diese „extremen Werte“ also nicht entfernen?
Wenn diese „extremen“ Werte problematisch sind, liegt es nahe, sie zu löschen und so unser Problem zu lösen. Dazu müssen wir formell definieren, was wir unter einem extremen Wert verstehen. Eine übliche Methode wäre die Hypothese, dass Daten der „Normalverteilung“ (auch Gaußsche Verteilung genannt) folgen. In diesem Fall würden alle Daten als „extrem“ betrachtet werden, die um mehr als das Dreifache der Standardabweichung vom Durchschnittswert abweichen. Bei unseren Daten liegt dieser Grenzwert bei rund 600 Euros, wodurch es einen Sinn ergeben würde, den „Longtail“ zu entfernen. Das Ergebnis entspricht jedoch nicht den Erwartungen. Wenn wir bei diesen „gefilterten“ Daten einen A/A-Test durchführen, erhalten wir folgendes Ergebnis:
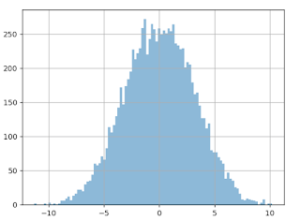
Die Verteilung der Differenzwerte des Durchschnittswerts ist genauso breit. Die Kurve hat sich kaum verändert.
Wenn wir jetzt einen A/B-Test durchführen (nach wie vor mit +3 Euro bei Version B), würden wir folgendes Ergebnis erhalten (siehe Grafik unten). Wir stellen in 17 % der Fälle eine negative Differenz fest (komplett das Gegenteil der Realität)! Obwohl wir die extremen Werte außer Acht gelassen haben. Und in 18 % der Fälle könnte man glauben, dass sich der Gewinn der Gruppe B auf mehr als 6 Euro beläuft, was doppelt so viel wie in Wirklichkeit ist!
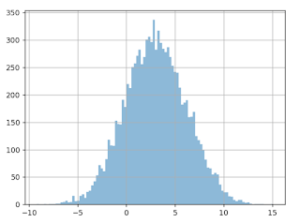
Warum funktioniert das nicht?
Weil die Daten für die Warenkorbwerte nicht der Normalverteilung folgen.
Im Folgenden wird der Approximationsfehler dargestellt:
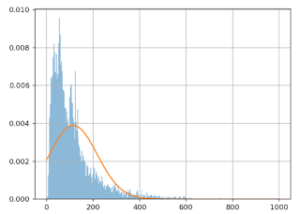
Die (horizontale) X-Achse zeigt die Warenkorbwerte; die (vertikale) Y-Achse wie oft dieser Wert bei diesen Daten festgestellt wurde.
Die blaue Linie stellt die effektiven Warenkorbwerte dar, die orangene Linie das Gaußsche Modell. Wir sehen deutlich, dass das Modell schlecht ist: die orangene Linie verläuft nicht parallel zur blauen Linie. Das Problem wird also nicht gelöst, wenn die extremen Werte einfach weggelassen werden.
Auch wenn wir im Vorfeld die Daten an das Gaußsche Gesetz „anpassen“ würden (also das Log der Warenkorbwerte nehmen), damit das Modell und die Daten deutlich besser aufeinander abgestimmt sind, würde das Problem nicht gelöst werden. Die Abweichung der verschiedenen Durchschnittswerte bleibt genauso groß.
Während eines A/B-Tests ist die Schätzung der Höhe des Wertzuwachses von großer Bedeutung, um die richtige Entscheidung zu treffen. Dies gilt vor allem, wenn mit der Gewinnervariante Kosten verbunden sind. Nach wie vor ist es heute schwierig, den durchschnittlichen Warenkorbwert genau zu berechnen. Die Wahl wird einzig nach Ihrem Konfidenzintervall getroffen, das nur die Existenz eines Gewinns (und nicht die Höhe) angibt. Sicherlich nicht ideal. Wenn sich aber Conversion Rate und durchschnittlicher Warenkorb in dieselbe Richtung bewegen, wird der Gewinn (oder Verlust) deutlich. Wenn beide nicht in dieselbe Richtung gehen, dann wird es schwierig oder sogar unmöglich, die angebrachte Entscheidung zu treffen.
Deshalb konzentrieren sich A/B-Tests hauptsächlich auf ergonomische oder designorientierte Tests von Websites, die sich weniger auf den durchschnittlichen Warenkorbwert auswirken, sondern eher auf die Conversion Rate. Daher sprechen wir hauptsächlich von „Conversion Rate-Optimierung“ (CRO) und nicht von „Business Optimization“. Jedes Experiment, das sich sowohl auf Conversion Rates als auch auf den durchschnittlichen Warenkorbwert auswirkt, lässt sich nur schwer analysieren. Genau hier ist es sinnvoll, einen technischen Spezialisten für die Conversion-Optimierung heranzuziehen, der Ihnen hilft, spezielle Tracking-Methoden einzurichten, die auf Ihr Upsell-Tool abgestimmt sind.
Um A/B-Tests in vollem Umfang zu verstehen, können Sie unseren Artikel lesen: „Das Problem ist die Wahl: Die Grenzen von A/B-Testing.







